Semana 30
semana 23
semana 22
semana 21
METACOGNICIÓN:
Responder las siguientes interrogantes:
¿Qué aprendí en esta sesión?
¿Cómo aprendí?
¿Qué dificultades tengo en la sesión?
¿Para qué me sirve lo aprendido?
SESIÓN Nº 12
AREA: RAZONAMIENTO LÓGICO MATEMÁTICO 2do. Grado: A, B, C, D, E, F
CONOCEMOS LA UTILIDAD DE LAS MAGNITUDES PROPORCIONALES EN DIVERSAS SITUACIONES.
EMPEZAMOS A DIVERTIRNOS:
NUESTRO PROPÓSITO:
¿QUÈ APRENDEREMOS HOY?
Utilizamos magnitudes proporcionales en diversas situaciones.
SITUACIÒN PROBLEMÀTICA
Resolución
Luego:
1. ¿Qué magnitudes intervienen en la situación significativa?
2. ¿Es correcto aplicar la multiplicación para entender la proporción de ambas magnitudes? Explica.
3. Describe otro procedimiento para dar respuesta a la pregunta significativa.
Observamos la tabla y respondemos la pregunta.
APRENDEMOS:
RELACIONES ENTRE DOS MAGNITUDES:
PROBLEMA.
Resolución:
· Según el enunciado, tenemos las magnitudes.
METACOGNICIÓN:
Responder las siguientes interrogantes:
¿Qué aprendí en esta sesión?
¿Cómo aprendí?
¿Qué dificultades tengo en la sesión?
¿Para qué me sirve lo aprendido?
Dinero
|
420
|
x
|
Días
|
7
|
15
|
Entonces:
TE INVITO A TRABAJAR EN TU LIBRO “RESOLVAMOS PROBLEMAS 2” DE LA PÀGINA N.º 30.
METACOGNICIÓN:
Responder las siguientes interrogantes:
¿Qué aprendí en esta sesión?
¿Cómo aprendí?
¿Qué dificultades tengo en la sesión?
SESIÓN Nº 11
AREA: RAZONAMIENTO LÓGICO MATEMÁTICO 2do. Grado: A, B, C, D, E, F
IDENTIFICAMOS MAGNITUDES PROPORCIONALES EN UN ALBERGUE PARA PERROS.
EMPEZAMOS A DIVERTIRNOS:
Magnitudes proporcionales
NUESTRO PROPÓSITO:
Establecemos relaciones entre datos de dos magnitudes y transformamos esas relaciones en proporcionalidad directa. También empleamos estrategias heurísticas y el procedimiento más conveniente a las condiciones del problema.
¿QUÈ APRENDEREMOS HOY?
Resolvemos situaciones diversas que involucran magnitudes proporcionales.
SITUACIÒN PROBLEMÀTICA
Albergamos perros sin hogar
Una asociación protectora de los animales acondiciona una casa para albergar a todos los perros que se encuentra abandonados en la calle. La asociación tiene dificultades para dar en adopción a perros adultos. Para promoverla, da a conocer el consumo de alimento de los perros buscando sensibilizar al público, ya sea para que adopten o donan alimentos. Se sabe que en el albergue hay 16 perros adultos y cada uno de ellos consume dos bolsas de alimento durante un mes.
Lee, razona y responda:
1. ¿Cuántas bolsas se necesitarán para alimentar a los 16 perros durante un mes?
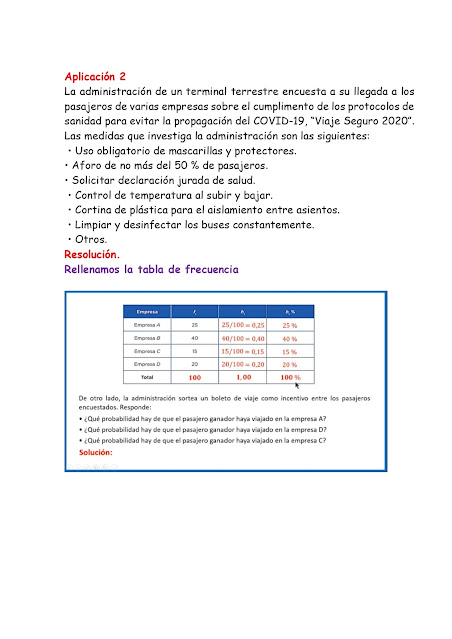
Para alimentar a los 16 perros se necesitarán 32 bolsas de alimento.
2. ¿Qué relación encuentras entre la cantidad de perros y la cantidad de bolsas de alimento?
La relación es de: La cantidad de perros es como 1 y la cantidad de alimentos es como 2. En este caso la relación siempre de 1 a 2.
3. Si llegan 4 perros adultos más al albergue ¿Cuántas bolsas de alimento se necesitarán a partir de este mes?
Para alimentar a los 20 perros se necesitarán 40 bolsas de alimentos.
APRENDEMOS:
MAGNITUD:
Es todo aquello que puede aumentar o disminuir su intensidad, y que se puede medir.
CANTIDAD:
Es el resultado de medir la variación de una magnitud en un determinado momento.
RELACIONES ENTRE DOS MAGNITUDES:
Dos magnitudes son proporcionales cuando, al variar una de ellas, la otra también varía en la misma proporción.
PROBLEMA.
Lidia puede leer un libro de 640 páginas en 40 días.
¿Cuántos días de demorará en leer un libro de 480hojas?
Resolución:
· Tengamos en cuenta que si lidia lee 480 hojas esto equivale a decir que lee 960 páginas.
· Según el enunciado, tenemos las magnitudes.
N.º de páginas
|
640
|
960
|
N.º de días
|
40
|
x
|
Entonces:
TE INVITO A TRABAJAR EN TU LIBRO “RESLOVAMOS PROBLEMAS 2” DE LA PÀGINA N.º 27,28 y 29.
METACOGNICIÓN:
Responder las siguientes interrogantes:
¿Qué aprendí en esta sesión?
¿Cómo aprendí?
¿Qué dificultades tengo en la sesión?
¿Para qué me serve lo aprendido?
SESIÓN 10
SESIÓN Nº 10
AREA: RAZONAMIENTO LÓGICO MATEMÁTICO 2do. Grado: A, B, C, D, E, F
INTERPRETAMOS GRÀFICOS QUE CONTIENEN NÙMEROS DECIMALES.
EMPEZAMOS A DIVERTIRNOS:
NUESTRO PROPÓSITO:
Resolvemos e interpretamos situaciones que involucran números decimales.
SITUACIÒN PROBLEMÀTICA SITUACIÒN PROBLEMÀTICA
La gráfica muestra la evolución del valor de compra y venta del dólar entre el 01 de junio y el 01 de julio. El eje vertical del precio del dólar en soles y el eje horizontal, el día del mes.
Lee, razona y responda:
a. ¿Entre qué días del mes los precios de compra y venta del dólar han tenido la mayor baja?
Los precios de compra y venta han tenido la mayor baja entre los días 5 y 7 de junio.
¿Qué día del mes los precios de compra y venta del dólar han tenido la mayor alza?
La mayor alza de los precios de compra y venta ha sido el día 23 de junio.
¿A qué conjunto numérico corresponde el valor de los precios del dólar?
Pertenece al conjunto de los números racionales, expresado como un número decimal exacto.
¿Qué significa 3,158 soles?
Significa 3 soles con 158 milésimas de sol.
¿Entre el 01/06 y el 01/07, qué días se gana más dinero en la compra y venta del dólar?
Los días 26, 27, 28 y 29 de junio.
b. ¿Cuánto sería tu ganancia máxima?
Para tener la máxima ganancia, hubieras comprado $1000 al precio de compra mínima el 05/06 y los hubieras vendido al precio de venta máxima el 23/06. Precio de compra: 1000 × 3,150 = S/3150 Precio de venta: 1000 × 3,180 = S/3180 Ganancia: S/3180 – S/3150 = S/30
APRENDEMOS:
Resolución:
METACOGNICIÓN:
Responder las siguientes interrogantes:
¿Qué aprendí en esta sesión?
AREA: RAZONAMIENTO LÓGICO MATEMÁTICO 2do. Grado: A, B, C, D, E, F
CALCULAMOS EL TOTAL A PAGAR POR UN SERVICIO DE SUMINISTRO ELÉCTRICO
Empezamos a divertirnos:
Los números decimales se encuentran en muchas cosas; por ejemplo, para expresar el tiempo que emplea un atleta en recorrer una pista atlética, las medidas de algún terreno, nuestra estatura, masa corporal, entre otros. Además, nuestra unidad monetaria es el sol (S/), pero también existen los céntimos. ¿Cómo podemos comparar dos de estas cantidades y de qué manera calculamos con ellas?
NUESTRO PROPÓSITO:
¿QUÉ APRENDEREMOS HOY?
Utilizamos los números decimales en nuestra vida diaria.
SITUACIÒN PROBLEMÀTICA
Observamos el recibo de l a señora Dina
SESIÓN Nº 10
AREA: RAZONAMIENTO LÓGICO MATEMÁTICO 2do. Grado: A, B, C, D, E, F
INTERPRETAMOS GRÀFICOS QUE CONTIENEN NÙMEROS DECIMALES.
EMPEZAMOS A DIVERTIRNOS:
Los números decimales
NUESTRO PROPÓSITO:
Establecemos relaciones entre datos y las transformamos en expresiones numéricas que incluyen operaciones con expresiones decimales. Así mismos justificamos con ejemplos las propiedades de las operaciones con decimales y corregimos errores si los hubiera.
¿QUÈ APRENDEREMOS HOY?
Resolvemos e interpretamos situaciones que involucran números decimales.
SITUACIÒN PROBLEMÀTICA SITUACIÒN PROBLEMÀTICA
Observa el grafico:
La gráfica muestra la evolución del valor de compra y venta del dólar entre el 01 de junio y el 01 de julio. El eje vertical del precio del dólar en soles y el eje horizontal, el día del mes.
Lee, razona y responda:
a. ¿Entre qué días del mes los precios de compra y venta del dólar han tenido la mayor baja?
Los precios de compra y venta han tenido la mayor baja entre los días 5 y 7 de junio.
¿Qué día del mes los precios de compra y venta del dólar han tenido la mayor alza?
La mayor alza de los precios de compra y venta ha sido el día 23 de junio.
¿A qué conjunto numérico corresponde el valor de los precios del dólar?
Pertenece al conjunto de los números racionales, expresado como un número decimal exacto.
¿Qué significa 3,158 soles?
Significa 3 soles con 158 milésimas de sol.
¿Entre el 01/06 y el 01/07, qué días se gana más dinero en la compra y venta del dólar?
Los días 26, 27, 28 y 29 de junio.
b. ¿Cuánto sería tu ganancia máxima?
Para tener la máxima ganancia, hubieras comprado $1000 al precio de compra mínima el 05/06 y los hubieras vendido al precio de venta máxima el 23/06. Precio de compra: 1000 × 3,150 = S/3150 Precio de venta: 1000 × 3,180 = S/3180 Ganancia: S/3180 – S/3150 = S/30
APRENDEMOS:
En estas actividades, tendrás el reto de interpretar gráficos, realizar comparaciones y operar con números racionales, para ello deberás emplear estrategias heurísticas y justificar los procedimientos que usaste.
PROBLEMA.
Tres amigos han ido a desayunar. Cada uno ha tomado una tostada y un zumo. Pagan en total 9,48 soles y saben que una tostada cuesta 1,25soles ¿Cuánto han pagado por cada zumo?
Resolución:
· Primero dividimos: El total entre la cantidad de amigos
9,48:3 = 3,16
· Ahora a este cociente le restamos lo que cuesta el zumo:
3,16 – 1,25 = 1,91
· Cada zumo cuesta 1,91soles.
TE INVITO A TRABAJAR EN TU LIBRO “RESLOVAMOS PROBLEMAS 2” DE LA PÀGINA N.º 46
METACOGNICIÓN:
Responder las siguientes interrogantes:
¿Qué aprendí en esta sesión?
Viendo el procedimiento de los problemas
¿Cómo aprendí?
Realizando problemas diferentes
¿Qué dificultades tengo en la sesión?
Confirmar mi resultado
¿Para qué me sirve lo aprendido?
Para resolver problemas que incluyan decimales
SESIÓN N. º 9
 |
| Añadir título |
Lee, razona y responda:
1. Cuanto es el consumo en kilovatios hora y cuanto fue el precio unitario en soles.
2. ¿Qué entiendes por Impuesto General a las Ventas? IGV.
3. Calcula el IGV en soles que corresponda al consumo de energía del mes actual.
4. Cual es el costo total del recibo en soles “ TOTAL DE MES ACTUAL”.
RESPONDEMOS:
1. El consumo en kilowatts hora es de 101 kW/h y el precio unitario es de 0,7141
2. La sigla IGV significa Impuesto General a las Ventas. Este tributo se impone a toda venta de bienes y servicios que se realiza en el Perú Este pago lo asume el consumidor final, suele incluirse en el precio de vente de los productos. Esto equivale al 18%.
3. Para hallar el 18% al consumo del mes, este se aplica al subtotal:
(18:100).85.21 = 15,3378 redondeando es:15,34
4. Para hallar el total se suma:
Cargo fijo………………………………………………………. 3,32
Cargo por reposición y mantenimiento……….. 1,10
Ene.Activa(s/.0,7141 x 101 KWh)………………………72,12
Alumbrado público………………………………………………… 8,28
Interés compensatorio……………………………………….. 0,39
SUBTOTAL…………………………………………………………….. 85,21
Imp.Gral a la Ventas………………………………………… 15,34
Cargo Energía ley MCTR 30468…………………… -9,42
Interés moratorio…………………………………………… 0,02
Saldo por redondeo……………………………………… -0,05
Aporte Ley Nº 28749…………………………………… 0,84
TOTAL A PAGAR………………………………………………… 91,90
APRENDEMOS:
Los números decimales se componen de cifras que son separadas de la parte entera con una coma, pero estas cifras tienen una característica que las diferencian según su posición. Las décimas se ubican después un lugar después de la coma; las centésimas están a dos lugares después del separador, las milésimas en el tercer lugar y así podríamos seguir con la diezmilésima, cienmilésimas, etc.
7,951
SE LEE: SIETE ENTEROS, NOVECIENTO CINCUENTA Y UN MILÈSIMOS
En el nùmero 7,951 notamos que 7 es la parte entera,9 es la dècima,5 es la centèsima y 1es la milèsima.
PROBLEMA.
La altura de una persona es de 1,85m y la de una torre es 26 veces la altura de la persona menos 1,009m. Halla la altura de la torre.
Resolución:
Altura de la persona:1,85m
Altura de la torre:26(1,85m) -1,009m = 47,091m.
TE INVITO A TRABAJAR EN TU LIBRO “RESOLVAMOS PROBLEMAS 2” DE LAS PÁGINAS Nº 47,48 y 49
METACOGNICIÓN:
Responder las siguientes interrogantes:
¿Qué aprendí en esta sesión?
¿Cómo aprendí?
¿Qué dificultades tengo en la sesión?
¿Para qué me sirve lo aprendido?
Para saber hallar respuestas decimales
SESIÓN N 08
SESIÓN N. º 8
AREA: RAZONAMIENTO LÓGICO MATEMÁTICO 2do. Grado: A, B, C, D, E, F
Empezamos a divertirnos:
Para empezar debemos recordar lo que tratamos en la sesion anterior; como hallamos el àrea y perìmetro de las diferentes figuras geomètricas. Asì mismo sus formulas.
Explique de forma escrita como hallarías el àrea y perìmetro:
Calculamos en diversas situaciones el àrea y perìmetro de figuras geomètricas.
Analizamos la situación planteada:
· Para calcular el área, haríamos por diferencia de áreas.
Área sombreada = área del rectángulo - el área de las dos semicircunferencias
· Para saber su perìmetro, se suma todas las longitudes de sus lados.
Así: 2p=suma de los dos lados del rectàngulo +la longitud de la circunferencia.
· Hallamos la longitud de la circunferencia.
· Para saber su perìmetro, se suma todas las longitudes de sus lados.
APRENDEMOS:
Ejemplo: Si el lado del cuadrado mide 10m, halle el àrea sombreada.
Resolución: Hallando el àrea sombreada por diferencia de àreas:
Así:
Ejemplo Halla el perìmetro de la region sombreada
SOLUCIÓN
SESIÓN N. º 8
AREA: RAZONAMIENTO LÓGICO MATEMÁTICO 2do. Grado: A, B, C, D, E, F
DETERMINAMOS EL ÀREA Y PERÌMETRO DE REGIONES POLIGONALES Y CIRCULARES.
Empezamos a divertirnos:
Para empezar debemos recordar lo que tratamos en la sesion anterior; como hallamos el àrea y perìmetro de las diferentes figuras geomètricas. Asì mismo sus formulas.
En la figura mostrada halla el àrea y perìmetro:
Explique de forma escrita como hallarías el àrea y perìmetro:
¿Qué aprenderemos hoy?
Calculamos el área y perímetro de figuras poligonales y circulares.
SITUACIÒN PROBLEMÀTICA
A continuación, te invitamos a dar respuesta a la situación “Regiones circulares y rectangulares). Dada la siguiente figura, halla el àrea y perìmetro de la figura sombreada; considerando el valor de (π = 3,14).
Sì: AB =9m Y AD=6m
Calculamos en diversas situaciones el àrea y perìmetro de figuras geomètricas.
· ¿Cuánto es el área total?
· ¿Cuánto es el perímetro?
Analizamos la situación planteada:
· Para calcular el área, haríamos por diferencia de áreas.
Área sombreada = área del rectángulo - el área de las dos semicircunferencias
Así: largo = 9m
Ancho = 6m
· Primero, hallamos el área del rectángulo
Entonces: Área = largo x Ancho
Área =9m x6m = 54M2
· Segundo, hallamos el área de las dos semicircunferencias:
Observación: Las dos semicircunferencias forman un círculo
· Para saber su perìmetro, se suma todas las longitudes de sus lados.
Así: 2p=suma de los dos lados del rectàngulo +la longitud de la circunferencia.
· Hallamos la longitud de la circunferencia.
· Para saber su perìmetro, se suma todas las longitudes de sus lados.
Así: 2p=suma de los dos lados del rectàngulo +la longitud de la circunferencia.
· Hallamos la longitud de la circunferencia.
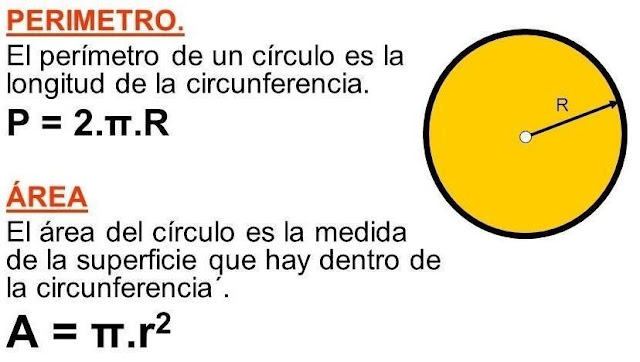
APRENDEMOS:
ÀREA: El área es la medida de la superficie encerrada en una superficie plana.
Ejemplo: Si el lado del cuadrado mide 10m, halle el àrea sombreada.
Resolución: Hallando el àrea sombreada por diferencia de àreas:
Así:
Ejemplo Halla el perìmetro de la region sombreada
π = 3,14✔
SESIÓN N° 7
DESCUBRIMOS PROPIEDADES ENTRE FORMAS GEOMÉTRICAS BIDIMENSIONALES, CALCULANDO SU PERÍMETRO Y ÁREA.
Empezamos a divertirnos:
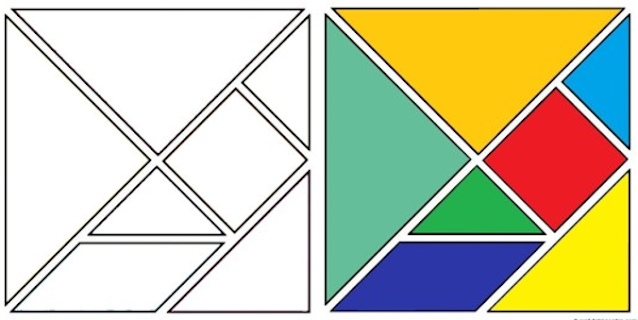
El tangram es un material útil para construir diversas figuras geométricas. Para las formas bidimensionales podemos determinar la medida de su contorno y medida de su superficie, para ello aplicamos los conceptos geométricos del perímetro y área. En estas actividades, tendrás el reto de representar formas bidimensionales con material concreto, dibujos y lenguaje geométrico; además, expresarás relaciones entre las propiedades del área y perímetro; emplearás estrategias heurísticas, recursos gráficos y procedimientos para determinar el perímetro y el área de figuras geométricas; y justificarás los procedimientos que usaste.
- Haciendo uso de todas las piezas del tangram, construye y representa dos figuras geométricas de tres lados que tengan igual perímetro e igual área.
- Forma un triángulo y un cuadrado con todas las piezas del tangram. Compara el área y el perímetro del triángulo y el cuadrado, y describe lo que observas.
¿Qué aprenderemos hoy?
Calcularás el perímetro y el área de diversas figuras geométricas.
SITUACIÓN PROBLEMÁTICA
Descubrimos propiedades entre formas geométricas bidimensionales, calculando su perìmetro y área.
El papá de Chamaquito le pide que le ayude a realizar unos cálculos para colocar cerámica en su piso para su cuarto, puesto que Chamaquito es muy talentoso para las matemáticas. Su papá le dice que le apoya para calcular su área cuyas medidas medidas son:2,70m de ancho y 3,90m de largo; además cada cerámica es de 30x30 cm.
- ¿Cuánto es el área total?
- ¿Cuánto es el perímetro?
- ¿Cuántas cerámicas se necesitan?
Analizamos la situación planteada:
- Para saber el área total solo basta multiplicar el largo por el ancho.
Así: largo=2,70m
Ancho=3,90m
Entonces: Área = largo x Ancho
Área =2,70m x3,90m =10,53m^2.
- Para saber su perímetro, se suma todas las longitudes de sus lados.
Así: 2,70m + 2,70m + 3,90m + 3,90m = 13,20m.
- Para calcular cuantas cerámicas e necesitan, dividimos:
Ancho: 30cm
Asì: 2,70cm: 30cm = 9 cerámicas
Asì: 3,90cm: 30cm = 13 cerámicas
Por lo tanto: 9x13=117 cerámicas
APRENDEMOS:
- ÁREA: El área es la medida de la superficie encerrada en una superficie plana.
- PERÍMETRO(2p): El perímetro es la suma de sus lados de una figura geométrica.
Ejemplo 1. Si el perímetro de la figura es 32m. Halla el valor de “a”.
Resolución: Hallando el perímetro.
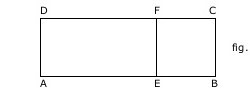
Ejemplo 2. En la figura el perímetro del rectángulo ABCD es 22m y EBCF un cuadrado de área 9 
Resolución: 
Entonces un lado es: L = 3, ya que EB=BC=CF=FE
· Finalmente, hallamos el área del rectángulo AEFD:
DESCUBRIMOS PROPIEDADES ENTRE FORMAS GEOMÉTRICAS BIDIMENSIONALES, CALCULANDO SU PERÍMETRO Y ÁREA.
Empezamos a divertirnos:
El tangram es un material útil para construir diversas figuras geométricas. Para las formas bidimensionales podemos determinar la medida de su contorno y medida de su superficie, para ello aplicamos los conceptos geométricos del perímetro y área. En estas actividades, tendrás el reto de representar formas bidimensionales con material concreto, dibujos y lenguaje geométrico; además, expresarás relaciones entre las propiedades del área y perímetro; emplearás estrategias heurísticas, recursos gráficos y procedimientos para determinar el perímetro y el área de figuras geométricas; y justificarás los procedimientos que usaste.
A partir de la situación, responde y realiza las siguientes preguntas (puedes responder de manera escrita u oral, grabando un audio):
- Haciendo uso de todas las piezas del tangram, construye y representa dos figuras geométricas de tres lados que tengan igual perímetro e igual área.
- Forma un triángulo y un cuadrado con todas las piezas del tangram. Compara el área y el perímetro del triángulo y el cuadrado, y describe lo que observas.
¿Qué aprenderemos hoy?
Calcularás el perímetro y el área de diversas figuras geométricas.
SITUACIÓN PROBLEMÁTICA
Descubrimos propiedades entre formas geométricas bidimensionales, calculando su perìmetro y área.
El papá de Chamaquito le pide que le ayude a realizar unos cálculos para colocar cerámica en su piso para su cuarto, puesto que Chamaquito es muy talentoso para las matemáticas. Su papá le dice que le apoya para calcular su área cuyas medidas medidas son:2,70m de ancho y 3,90m de largo; además cada cerámica es de 30x30 cm.
- ¿Cuánto es el área total?
- ¿Cuánto es el perímetro?
- ¿Cuántas cerámicas se necesitan?
Analizamos la situación planteada:
- Para saber el área total solo basta multiplicar el largo por el ancho.
Así: largo=2,70m
Ancho=3,90m
Entonces: Área = largo x Ancho
Área =2,70m x3,90m =10,53m^2.
- Para saber su perímetro, se suma todas las longitudes de sus lados.
Así: 2,70m + 2,70m + 3,90m + 3,90m = 13,20m.
- Para calcular cuantas cerámicas e necesitan, dividimos:
Ancho: 30cm
Asì: 2,70cm: 30cm = 9 cerámicas
Asì: 3,90cm: 30cm = 13 cerámicas
Por lo tanto: 9x13=117 cerámicas
APRENDEMOS:
- ÁREA: El área es la medida de la superficie encerrada en una superficie plana.
- PERÍMETRO(2p): El perímetro es la suma de sus lados de una figura geométrica.
Ejemplo 1. Si el perímetro de la figura es 32m. Halla el valor de “a”.
Resolución: Hallando el perímetro.
2p =3+4+12+a
32=19+a
32-19=a
13=a
Ejemplo 2. En la figura el perímetro del rectángulo ABCD es 22m y EBCF un cuadrado de área 9
Resolución:
· Primero hallamos el lado del cuadrado EBCF:
Como el área es 9 m2
Entonces hallamos uno de sus lados:
Área= lado x lado
Entonces un lado es: L = 3, ya que EB=BC=CF=FE
· Como el perímetro es igual a la suma de sus lados:
2p=AE+EF+FD+AD; ADEMÁS FD=AE =b
22=b+3+b+3
22=2b+6
22-6=2b
16=2b
8=b.
· Finalmente, hallamos el área del rectángulo AEFD:
Sabemos por fórmula que el área del rectángulo es, largo por ancho.
Como ya hallamos los lados de rectángulo AEFD, cuyas medidas son:
Razonamiento Lógico Matemático 2do. A, B, C, D, E, F
SESIÓN N° 6
ÁREA: RAZONAMIENTO LÓGICO MATEMÁTICO 2 GRADO: A, B, C, D, E, F
¿Cómo empezamos?
Determinamos la distancia recorrida por un ciclista
SITUACIÓN SIGNIFICATIVA:
A partir de esta situación responde la siguiente pregunta:
- EL primer segundo: 3m
- El segundo segundo: 6m
- EL tercer segundo: 9m
- El cuarto segundo: 12m y así sucesivamente hasta los 10 segundos.
Entonces:
- La suma total de su recorrido será:
- Si sumamos el primer término con el último resulta: 3+30=33
- Si sumamos el segundo término con el penúltimo resulta: 6+27=33
- Si sumamos el tercer término con el antepenúltimo resulta: 9+24=33
Y así sucesivamente siempre nos resultará 33. Finalmente multiplicamos por 5 pares, resultando 165m.
Donde:
- Suma de lo “n” términos de una progresión aritmética.
- último término de una progresión aritmética.
- Primer término de una progresión aritmética.
- Número de términos de una progresión aritmética.
SOLUCIÓN:
Respuesta: La distancia recorrida es de 165m.
Ejemplo 1.
Las siguientes figuras han sido construidas con palitos de fósforo:
¿Cuántos palitos de fósforo se necesitan para formar una figura con 15 hexágonos?
Resolución:
Si la P.A.: 6;11;16; 21; …………
ÁREA: RAZONAMIENTO LÓGICO MATEMÁTICO 2 GRADO: A, B, C, D, E, F
¿Cómo empezamos?
Determinamos la distancia recorrida por un ciclista
SITUACIÓN SIGNIFICATIVA:
Un ciclista baja por una pendiente acelerando su bicicleta. En el primer segundo recorre 3 m; en el siguiente segundo, 6 m; en el tercero, 9 m; en el cuarto, 12 m; y así sucesivamente.
A partir de esta situación responde la siguiente pregunta:
Si llega hasta la parte baja de la pendiente en 10 segundos, ¿cuál es la distancia total recorrida?
VEAMOS ENTONCES COMO PODEMOS CALCULAR LA DISTANCIA TOTAL RECORRIDA:
- EL primer segundo: 3m
- El segundo segundo: 6m
- EL tercer segundo: 9m
- El cuarto segundo: 12m y así sucesivamente hasta los 10 segundos.
Entonces:
- La suma total de su recorrido será:
- Si sumamos el primer término con el último resulta: 3+30=33
- Si sumamos el segundo término con el penúltimo resulta: 6+27=33
- Si sumamos el tercer término con el antepenúltimo resulta: 9+24=33
Y así sucesivamente siempre nos resultará 33. Finalmente multiplicamos por 5 pares, resultando 165m.
LA SUMA DE LOS “n” TÉRMINOS DE UNA PROGRESIÓN ARITMÉTICA
Donde:
- Suma de lo “n” términos de una progresión aritmética.
- último término de una progresión aritmética.
- Primer término de una progresión aritmética.
- Número de términos de una progresión aritmética.
SOLUCIÓN:
Si la P.A.: 3;6;9; 12; …………
Respuesta: La distancia recorrida es de 165m.
Las siguientes figuras han sido construidas con palitos de fósforo:
¿Cuántos palitos de fósforo se necesitan para formar una figura con 15 hexágonos?
Resolución:
Si la P.A.: 6;11;16; 21; …………
RAZONAMIENTO LÓGICO MATEMÁTICO 2do
SESIÓN 5
AREA: RAZONAMIENTO LÓGICO MATEMÁTICO 2do. Grado: A, B, C, D, E, F
DOCENTE: EDGARDO ESQUIVEL NUÑEZ
I. ¿Cómo empezamos?
DETERMINAMOS LA CANTIDAD DE BLOQUES PARA UNA ESCALERA APLICANDO LAS PROGRESIONES ARITMÉTICAS
SITUACIÓN SIGNIFICATIVA
El alcalde de un distrito de Lima va a construir escaleras con bloques de cemento, como se muestra en la figura.
¿Cuántos bloques de cemento se necesitarán para construir una escalera de 240 escalones?
Para desarrollar la situación significativa necesitamos conocer lo siguiente:
PROPÓSITO: Representamos nuestra comprensión sobre la regla de formación de progresiones aritméticas, estableciendo relaciones entre dichas representaciones. Asimismo, justificamos con ejemplos y con nuestros conocimientos matemáticos la posición de un término de una progresión aritmética y su regla de formación; además, resolvemos problemas de la suma de términos de una progresión aritmética y corregimos errores si los hubiera
DONDE:
ENTONCES PODEMOS AFIRMAR QUE:
DEFINICIÒN
Una progresión aritmética es una sucesión en la que cada término se obtiene sumando al anterior una cantidad fija llamada diferencia o razón aritmética.
La diferencia de una progresión aritmética se halla restando un término menos el anterior.
El último libro cuesta $15,5.
METACOGNCIÓN:
1. ¿Qué aprendí?
2. ¿Para qué aprendí?
3. ¿Qué dificultades tuve al desarrollar la sesión?
EVALUACIÓN : Da le clic en su sección- seleccione su nombre y la contraseña e su DNI.
¡LISTO AMIGOS! AHORA TE INVITO A DESARROLLAR LAS PAGINAS 186 Y 187 DEL LIBRO “RESOLVAMOS PPROBLEMAS 2” DEL MINEDU
TODA CONSULTA O ENVIO DE EVIDENCIA AL PROFESOR EDGARDO ESQUIVEL NUÑEZ
WhatsApp Nro. 975758008_____________________________________________
PROGRAMA DE EDUCACIÓN A DISTANCIA
SESIÓN Nro. 4
AREA: RAZONAMIENTO LÓGICO MATEMÁTICO 2do. Grado: A, B, C, D, E, F
I. ¿Cómo empezamos?
EXPRESAMOS CANTIDADES MUY GRANDES
Y MUY PEQUEÑAS
NOTACIÓN CIENTIFICA
La notación científica nos permite escribir números muy grandes o muy pequeños de forma abreviada. Esta notación consiste simplemente en multiplicar por una POTENCIA DE BASE 10 con exponente positivo o negativo.
OBSERVAMOS LO SIGUIENTE:
¿Puedes realizar algunos ejemplos?
LA MULTIPLICACIÓN POR 10 CON EXPONENTE POSITIVO:
Al multiplicar un número por la potencia 10n (con exponente positivo) se desplaza la coma hacia la derecha tantas posiciones como indica el exponente.
LA MULTIPLICACIÓN POR 10 CON EXPONENTE NEGATIVO
Al multiplicar un número por la potencia 10-n (con exponente negativo) se desplaza la coma hacia la izquierda tantas posiciones como indica el exponente (al cambiarle el signo).
¿Conoces estas expresiones?
¿Cómo utilizarías estas expresiones?
EVALUACIÓN : Da le clic en su sección- seleccione su nombre y la contraseña e su DNI.
Toda consulta o envío al WhatsApp 942508752
CARLOS QUINTO ROJAS
_________________________________________________________________________________
SESION 03
INSTITUCIÓN EDUCATIVA “JOSÉ MARÍA ARGUEDAS”
INSTITUCIÓN EDUCATIVA “JOSÉ MARÍA ARGUEDAS”
PROGRAMA DE EDUCACIÓN A DISTANCIA
AREA: RAZONAMIENTO LÓGICO MATEMÁTICO” 2do. Grado: A, B, C, D, E, F
Juguemos un poco con los números:
64 , 32 , 16 , 8 , 4 , 2 , 1 , ½ , ¼
RESPONDE: __________________________________________________________________________
Sacar conclusiones de este grupo de números te ayudará a entender la situación problemática que se plantea
También debemos recordar que:
Ahora si empecemos:
Resolver el siguiente problemas y la solución enviarlo con sus respectivos nombres - secciones y subirlos por whatsApp 942508752 o enviarlos al correo krlosquintorojas@gmail.com
EVALUACION: dale clic en su grado seleccione su nombre su contraseña es su dni.
SEGUNDO A
SEGUNDO B
SEGUNDO C
SEGUNDO D
SEGUNDO E
SEGUNDO F
SEGUNDO A
SEGUNDO B
SEGUNDO C
SEGUNDO D
SEGUNDO E
SEGUNDO F
_____________________________________________________________________________
SESIÓN Nº 2 RAZ MATEMÁTICO "SEGUNDO GRADO"
Organizando los datos de masa corporal
¡Hola!
Gracias por conectarte y ser parte de Aprendo en casa.
¿Cómo podrías organizar los valores de la masa corporal de tus familiares? ¿Entre qué valores se encuentra la mayor parte de tus familiares?
Pues hoy lo sabremos.
¡Empecemos!
Aprenderás a procesar datos, organizando la información en tablas. También realizarás histogramas para representar la información y polígonos de frecuencia que te permiten interpretar información. Finalmente, podrás elaborar conclusiones justificándolas sobre la base de conocimientos estadísticos.
Tienes 40 minutos para realizar cada actividad de esta guía.
¿Preparada(o)?
¡ATENTA(O)!, QUE AQUÍ ENTRAMOS DE LLENO AL DESARROLLO
El profesor de Educación Física pesa a sus estudiantes para actualizar sus fichas personales y, luego, registra los datos en una libreta:
Abril: 45,7 kg
|
Nell: 70,1 kg
|
Álex: 55,8 kg
|
Edgar: 65,8 kg
|
Tomás P.: 51,4 kg
|
Carlos A.:76 kg
|
Hugo: 71,4 kg
|
Martín: 75,4 kg
|
Aníbal: 50,6 kg
|
Carlos S.: 57 kg
|
María: 46kg
|
Mónica: 41 kg
|
Luis: 60,4 kg
|
Luisa: 49,4 kg
|
Laura: 49,4 kg
|
Linda: 49,4 kg
|
Lucía: 46,8 kg
|
Luna: 56,9 kg
|
Silvia T.: 42,8 kg
|
Enrique: 66,8 kg
|
Noemí: 40,7 kg
|
Norma: 42,7 kg
|
Paola: 50,7 kg
|
Silvia A.: 40,7 kg
|
Teresa: 50,5 kg
|
Tomás R.: 70,5 kg
|
Tito: 70,5 kg
|
Ricardo: 73,5 kg
|
Melquíades: 60,5 kg
|
Tomás B.: 50,5 kg
|
Jesús: 80kg
|
Mirtha: 50,3 kg
|
A partir de la situación, expresa el comportamiento de estos datos mediante un histograma y de acuerdo con la lectura del gráfico determina:
1. ¿Entre qué valores varía la masa corporal (MC) de la mayoría de estudiantes?
2. ¿Y qué cantidad tiene masa corporal (MC) igual o mayor que 61,7 kg?
Veamos juntos la solución que se encuentra en la ficha “Solución Matemática 2” de la semana 2, en la sección “Recursos” de esta plataforma.
¿QUÉ ES EL IMC?
El índice de masa corporal (IMC) es un método utilizado para estimar la cantidad de grasa corporal que tiene una persona, y determinar por tanto si el peso está dentro del rango normal, o por el contrario, se tiene sobrepeso o delgadez. Para ello, se pone en relación la estatura y el peso actual del individuo. Esta fórmula matemática fue ideada por el estadístico belga Adolphe Quetelet, por lo que también se conoce como índice de Quetelet o Body Mass Index (BMI).
PARA TENER EN CUENTA:
Actualmente, esta fórmula está cayendo en desuso porque se está viendo que el IMC no hace diferencia entre la grasa corporal y la muscular, lo que hace que no sea muy exacto. “Un deportista o un culturista van a tener siempre un sobrepeso si tenemos en cuenta su peso respecto a la altura, pero no tienen los problemas de salud que tiene una persona obesa. Esta última tiene problemas debido a la cantidad de grasa que tienen, no por el peso”, explica Carmen Escalada, nutricionista del Instituto Médico Europeo de la Obesidad (IMEO). La cantidad de grasa marca mejor nuestro estado de salud
Actividad Familiar
1. Obtén tu peso en kilogramos
2. Averigua cual es tu talla o altura
3. Calcula tu índice de masa corporal
4. Ahora has el calculo de los integrantes de tu familia y haz un análisis con el cuadro siguiente
RETROALIMENTACIÓN:
Resumen de los aprendido sobre el IMC
METACOGNICIÓN:
Luego responden:
¿Qué preguntas te fueron difíciles?
¿Para qué será importante lo que aprendí?
¿Cómo puedo aplicarlo en la vida diaria?
* PUEDE REALIZAR SU TRABAJO EN HOJAS O USAR MS. WORD ENVIAR LA EVIDENCIA DE FOTOS O ARCHIVOS.
Resolver el siguiente problemas y la solución enviarlo con sus respectivos nombres - secciones y subirlos por whatsApp 942508752 o enviarlos al correo krlosquintorojas@gmail.com
SESIÓN DE APRENDIZAJE N° 1
MOTIVACIÓN - SABERES PREVIOS:
Se pide a los estudiantes que observen el vídeo.
¿ De que trata el vídeo?
¿ Cual es la importancia ?
¿ Que mensaje nos trae ?
Se les recuerda a los estudiantes el propósito: El estudiante escucha las indicaciones del docente, y proceden a realizar un Trabajo individualizado dónde resuelven problemas, empleando diversas materiales a su alcance en casa y que lo servirá en la vida diaria.
Luego de resolver, se plantea las siguientes preguntas:
- ¿Qué dificultad tuvieron al desarrollar?
- ¿Qué pregunta te fue muy difícil?
- ¿Cuál de estas preguntas te fue más fácil en resolver?
Con los datos obtenidos, realizamos las respuestas correspondientes.
Resolver el siguiente problemas y la solución enviarlo con sus respectivos nombres - secciones y subirlos por whatsApp 942508752 o enviarlos al correo krlosquintorojas@gmail.com
EVALUACIÓN:
Entrega de sus trabajos.
RETROALIMENTACIÓN:
Resumen de los aprendido sobre muestra
METACOGNICIÓN:
Luego responden:
¿Qué preguntas te fueron difíciles?
¿Para qué será importante lo que aprendí?
¿Cómo puedo aplicarlo en la vida diaria?
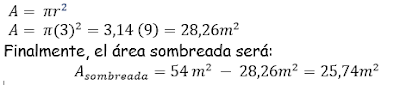
No hay comentarios.:
Publicar un comentario