SESIÓN 12 MATEMÁTICA
SESIÓN 34 - SEMANA 35 MATEMÁTICA
PROGRAMA DE EDUCACIÓN A DISTANCIA
SESIÓN DE APRENDIZAJE – SEMANA 35
ÁREA DE MATEMÁTICA
SEGUNDO: A - B - C - D – E – F.
DOCENTES: CABELLO MELO, MAURO
RAMOS FLORES, JESSICA
Competencia: Resolución de problemas de forma movimiento y localización.
TÍTULO DE LA SESIÓN
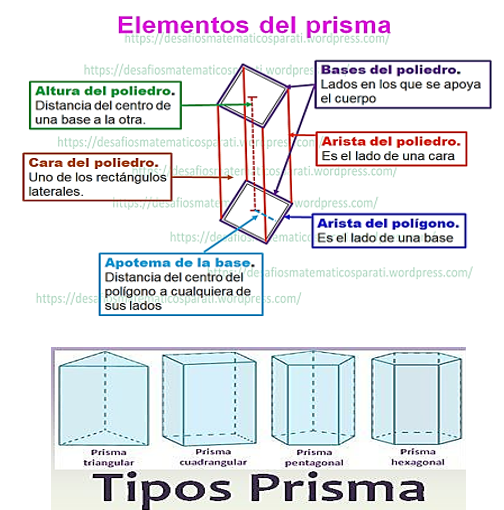
RELACIONAMOS LAS PROPIEDADES DEL PRISMA Y CILINDRO EN OBJETOS REUTILIZADOS
¿QUÉ APRENDERÉ HOY?
¿CÓMO EMPEZAMOS?
Estimados estudiantes iniciaremos viendo las siguientes imágenes y algunos ejercicios.
¿Qué forma tiene la base del cilindro?
……………………………………………………………………
¿Qué forma tiene la base un prisma?
………………………………………………………………………….
¿Qué elementos tiene el cilindro?
………………………………………………………………………….
¿Qué formula se utiliza para determinar al área de un hexagonal?
………………………………………………………………………….
¿QUÉ HARÉ?:
AHORA RESOLVEREMOS ALGUNAS SITUACIONES DE LA VIDA COTIDIANA
SITUACIÓN PROBLEMÁTICA 1.
Un estudiante del segundo grado desea saber cuál es el área lateral, total y el volumen del cilindro que se muestra.
SOLUCIÓN
Situación 2
Mariela tiene un regalo de forma un prisma pentagonal, y desea saber cuál es su medida de sus áreas y de su volumen, de la figura que se muestra.
SOLUCIÓN
Situación 3
El alcalde del distrito de Santa Rosa de Sacco, en unos de sus proyectos desea construir la glorieta del parque como la mostrada en la figura. Para armar la estructura, Diego utiliza tubos de acero. Cada barra de estos tubos tiene una longitud de 6 m.
1. ¿Cuántos metros de tubo de acero se necesitan para los parantes de la glorieta?
2. ¿Cuántos metros de tubo de acero se necesitarán para los bordes de la base del techo?
3. ¿Cómo hallarías el área de la base de la glorieta?
SOLUCIÓN
1. ¿Cuántos metros de tubo de acero se necesitan para los parantes de la glorieta?
Se observa que cada parante de la glorieta mide 2,50 m.
v Por lo tanto. Parante: 6 x 2,50 m = 15 m
Respuesta: Para los parantes de la glorieta se necesitan 15 m. de tubos
2. ¿Cuántos metros de tubo de acero se necesitarán para los bordes de la base del techo?
v Se observa que el borde del techo tiene la forma de un hexágono del lado 2,40 m.
v Por lo tanto, el borde del techo: 2,40 m x 6 = 14,4 m.
Respuesta: Para los bordes de la base del techo se necesita 14,40 m. de tubos.
3. ¿Cómo hallarías el área de la base de la glorieta?
Situación 4
Lucy tiene una caja de forma de prisma rectangular recto, cuya altura mide 7 cm; su ancho, 12 cm y el largo, 15 cm. Ella desea forrarla para guardar sus materiales escolares. Calcula el área total de papel reutilizados que necesita para forrar la caja, sin considerar otros detalles como pestañas laterales o dobleces.
SOLUCIÓN
Hallamos el área de la base Calculamos el perímetro
Calculamos el área lateral Calculamos el área total
PROGRAMA DE EDUCACIÓN A DISTANCIA
SEGUNDO: A - B - C - D – E – F.
TÍTULO DE LA SESIÓN
RESOLVEMOS SITUACIONES DIVERSAS QUE INVOLUCRAN MAGNITUDES PROPORCIONALES
¿CÓMO EMPEZAMOS?
a. ¿De qué datos se dispone en la situación?
b. ¿Qué magnitudes intervienen en la situación?
c. ¿Qué te piden hallar en la pregunta de la situación? ……………………………………………………………………………
¿QUÉ APRENDERÉ HOY?
¿QUÉ HARÉ?
Ahora resolveremos la siguiente situación problemática.
2. Un poste produce una sombra de 4,5 m en el piso. Si en el mismo instante una varilla vertical de 49 cm genera una sombra de 63 cm, ¿cuál es la altura del poste?
3. La gráfica muestra la cantidad de dinero que emplea el tutor de segundo grado "A" para adquirir las entradas de sus estudiantes en la visita al Museo de Historia Natural. Traslada los valores y completa la tabla. ¿Cuál es el precio de una entrada al museo? Justifica tu respuesta.
CANTIDAD DE ESTUDIANTES
5
8
12
15
COSTO DE ENTRADAS
10
a
b
30
De la tabla:
CANTIDAD DE ESTUDIANTES
5
8
12
15
COSTO DE ENTRADAS
10
16
24
30
Respuesta: El precio de la entrada al museo es de S/ 2
PROGRAMA DE EDUCACIÓN A DISTANCIA
SESIÓN DE APRENDIZAJE – SEMANA 35
ÁREA DE MATEMÁTICA
SEGUNDO: A - B - C - D – E – F.
DOCENTES: CABELLO MELO, MAURO
RAMOS FLORES, JESSICA
Competencia: Resolución de problemas de forma movimiento y localización.
TÍTULO DE LA SESIÓN
RELACIONAMOS LAS PROPIEDADES DEL PRISMA Y CILINDRO EN OBJETOS REUTILIZADOS
¿QUÉ APRENDERÉ HOY?
¿CÓMO EMPEZAMOS?
Estimados estudiantes iniciaremos viendo las siguientes imágenes y algunos ejercicios.
¿Qué forma tiene la base del cilindro?
……………………………………………………………………
¿Qué forma tiene la base un prisma?
………………………………………………………………………….
¿Qué elementos tiene el cilindro?
………………………………………………………………………….
¿Qué formula se utiliza para determinar al área de un hexagonal?
………………………………………………………………………….
¿QUÉ HARÉ?:
AHORA RESOLVEREMOS ALGUNAS SITUACIONES DE LA VIDA COTIDIANA
SITUACIÓN PROBLEMÁTICA 1.
Un estudiante del segundo grado desea saber cuál es el área lateral, total y el volumen del cilindro que se muestra.
SOLUCIÓN
Situación 2
Mariela tiene un regalo de forma un prisma pentagonal, y desea saber cuál es su medida de sus áreas y de su volumen, de la figura que se muestra.
SOLUCIÓN
Situación 3
El alcalde del distrito de Santa Rosa de Sacco, en unos de sus proyectos desea construir la glorieta del parque como la mostrada en la figura. Para armar la estructura, Diego utiliza tubos de acero. Cada barra de estos tubos tiene una longitud de 6 m.
1. ¿Cuántos metros de tubo de acero se necesitan para los parantes de la glorieta?
2. ¿Cuántos metros de tubo de acero se necesitarán para los bordes de la base del techo?
3. ¿Cómo hallarías el área de la base de la glorieta?
SOLUCIÓN
1. ¿Cuántos metros de tubo de acero se necesitan para los parantes de la glorieta?
Se observa que cada parante de la glorieta mide 2,50 m.
v Por lo tanto. Parante: 6 x 2,50 m = 15 m
Respuesta: Para los parantes de la glorieta se necesitan 15 m. de tubos
2. ¿Cuántos metros de tubo de acero se necesitarán para los bordes de la base del techo?
v Se observa que el borde del techo tiene la forma de un hexágono del lado 2,40 m.
v Por lo tanto, el borde del techo: 2,40 m x 6 = 14,4 m.
Respuesta: Para los bordes de la base del techo se necesita 14,40 m. de tubos.
3. ¿Cómo hallarías el área de la base de la glorieta?
Situación 4
Lucy tiene una caja de forma de prisma rectangular recto, cuya altura mide 7 cm; su ancho, 12 cm y el largo, 15 cm. Ella desea forrarla para guardar sus materiales escolares. Calcula el área total de papel reutilizados que necesita para forrar la caja, sin considerar otros detalles como pestañas laterales o dobleces.
SOLUCIÓN
Hallamos el área de la base Calculamos el perímetro
Calculamos el área lateral Calculamos el área total
CANTIDAD DE ESTUDIANTES
|
5
|
8
|
12
|
15
|
COSTO DE ENTRADAS
|
10
|
a
|
b
|
30
|
CANTIDAD DE ESTUDIANTES
|
5
|
8
|
12
|
15
|
COSTO DE ENTRADAS
|
10
|
16
|
24
|
30
|
SESIÓN 11 - MATEMÁTICA
PROGRAMA DE EDUCACIÓN A DISTANCIA
ÁREA DE MATEMÁTICA
SEGUNDO: A - B - C - D – E – F.
TÍTULO DE LA SESIÓN
RESOLVEMOS SITUACIONES DIVERSAS QUE INVOLUCRAN MAGNITUDES PROPORCIONALES
Ahora ya nos podemos hacer la siguiente pregunta. ¿Qué son magnitudes directamente proporcionales?
Piensa en la siguiente situación:
El profesor de matemáticas tiene un montón de exámenes que corregir, pero prefiere dedicar bastante tiempo a cada examen para no cometer errores. Después de varias horas, se ha dado cuenta de que corrige 3 exámenes por hora.
Como puedes observar, al multiplicar una magnitud por un número, la otra resulta multiplicada por ese mismo número. Lo mismo sucede si dividimos.
DEFINICIÒN: Dos magnitudes se dicen directamente proporcionales si al multiplicar (dividir) una de ellas por un número distinto de cero, la otra resulta multiplicada (dividida) por ese mismo número.
AHORA RESPONDE LAS SIGUIENTES INTERROGANTES:
a. ¿Qué es una magnitud?
b. ¿Cuáles son las magnitudes que se presenta el docente en la situación problemática?
c. ¿Para usted qué es proporcionalidad directa, según la definición? ……………………………………………………………………………
¿QUÉ APRENDERÉ HOY?
Resuelve problemas empleando proporcionalidad directa, empleando estrategias heurísticas, y procedimientos pertinentes para resolver problemas de la vida diaria.
¿QUÉ HARÉ?:
Ahora resolveremos la siguiente situación problemática.
Vídeo juegos
2
5
Costo
80
x
Respuesta: Los 5 vídeos juegos costara 200 soles.
Latas
1 200
X
Horas
8
5
Respuesta: En 5 horas de trabajo realizarán 75 latas de refresco.
3. Marco registra en una tabla la cantidad de rosas que compra y el monto de dinero que pagó.
rosas (unidades)
4
10
9
20
pagado (soles)
10
25
22,5
50
¿Cuánto pagará Marco por las 37 rosas que comp
Resolución:
rosas
9
37
soles
22,5
x
O también:
rosas
4
37
soles
10
x
Vídeo juegos
|
2
|
5
|
Costo
|
80
|
x
|
Latas
|
1 200
|
X
|
Horas
|
8
|
5
|
rosas (unidades)
|
4
|
10
|
9
|
20
|
pagado (soles)
|
10
|
25
|
22,5
|
50
|
rosas
|
9
|
37
|
soles
|
22,5
|
x
|
rosas
|
4
|
37
|
soles
|
10
|
x
|
SESIÓN 10 MATEMÁTICA

PROGRAMA DE EDUCACIÓN A DISTANCIA
SESIÓN DE APRENDIZAJE N° 10
SEGUNDO: A - B - C - D – E – F.
TÍTULO DE LA SESIÓN
Resolvemos e interpretamos situaciones que involucran números decimales.
¿CÓMO EMPEZAMOS?
Buenos días mis estimados estudiantes, felicitarle por el buen trabajo realizado en la sesión anterior, en esta nueva sesión seguiremos aprendiendo el tema de números decimales y para ello te mostraré la siguiente imagen.
AHORA RESPONDE LAS SIGUIENTES INTERROGANTES:
a. ¿Qué representa las líneas de color rojo en la gráfica?
b. ¿Qué representa las líneas de color verde en la gráfica? …………………………………………………………………..…………………
c. Observa los datos en el eje horizontal (días), ¿Cuál es la razón aritmética entre fecha y fecha?
Resuelve problemas con números decimales, estableciendo relaciones entre gráficos, y aplicando operaciones con expresiones decimales, para emplearlos en la solución de problemas de la vida diaria.
¿QUÉ HARE?:
Ahora resolveremos las siguientes situaciones problemáticas.
1. Ana se dedica a la compra y venta de dólares y el día 15 de junio compra
Resolución:
Para saber cuántos soles invierte en la compra de $15 000, debemos trazar una línea vertical que una la fecha 15/06 con el inicio de la línea verde.
Ha invertido S/ 51 390.
El 21/06 el precio de venta del dólar es de S/ 3,442. Entonces, para saber
cuanto recibió Ana, multiplicamos este valor por 15 000:
3,442 × 15 000 = 51 630
Termino de la venta del dólar S/ 51 630.
El monto recaudado al finalizar la venta del dólar es mayor que el monto invertido; por lo tanto, Ana ganó.
51 630 – 51 390 = 240
Respuesta: El monto que gano fue de S/ 240.
2. En Los años 2012/2013 los países que a continuación se describe tuvieron un incremento en la producción de café, teniendo el siguiente resultado: Brasil tuvo un incremento de 50,8, Vietnam de 2,2; Colombia en 9,50; Indonesia 50,8 y Etiopia en 8,1. Compara los datos con el siguiente gráfico, con los mismos países. Luego responde: ¿Qué país ha tenido el mayor incremento de la producción de café entre los periodos 2012/2013 a 2015/2016?
SOLUCIÓN
Para el periodo 2012/2013 a 2015/2016, organizo la información en la siguiente tabla:
País
Producción de café en millones de sacos de 60 kg
2012/2013
2015/2016
Incremento
Brasil
50,8
49,4
-1,4
Vietnam
22,0
29,3
7,3
Colombia
9,50
13,6
4,1
Indonesia
50,8
11,8
-39
Etiopía
8,1
6,5
-1,6
Para sacar el incremento se realiza de la siguiente manera:
49,4
–
50,8
=
- 1,4
La producción de café en Brasil fue disminuyendo, con respecto a los países de Vietnam y Colombia.
29,3
–
22,0
=
7,3
La producción de café en Vietnam fue en ascenso, con relación a los demás países.
13,6
–
9,50
=
4,1
La producción de café de Colombia también fue creciendo, pero menos que Vietnam.
11,8
–
50,80
=
- 3,9
Su producción de café de Indonesia fue mucho más la disminución, con relación a los demás países.
6,5
–
8,1
=
- 1,6
Etiopia fue disminuyendo, pero no es el último en la producción de café.
Respuesta: Vietnam ha tenido el mayor incremento en la producción de café.
SESIÓN DE APRENDIZAJE N° 9
SEGUNDO: A - B - C - D – E – F.
TÍTULO DE LA SESIÓN
AHORA RESPONDE LAS SIGUIENTES INTERROGANTES:
a. ¿Cuánto fue el consumo en kilovatios hora (kWh)?
b. En la actualidad, ¿cuánto es el porcentaje que se aplica por concepto de IGV?
…………………………………………………………………
c. Para calcular el "Total Importes", ¿qué datos requieres?
d. ¿Cuál es el costo en soles de "Total del mes actual"?
e. Con los datos encontrados, ¿qué tema se trata en esta sesión?
Resuelve problemas con números decimales aplicando estrategias heurísticas y procedimientos, para que lo puedan aplicar en la solución de problemas de la vida diaria.
¿QUÉ HARÉ?:
Ahora resolveremos las siguientes situaciones problemáticas.
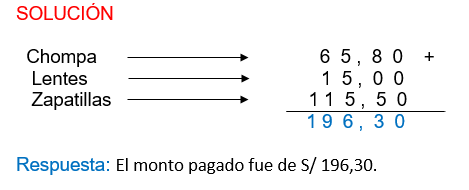
1. Manuela visita una tienda de ropas y compra las prendas (chompa, zapatillas y lentes) que se presenta en la imagen, ¿Cuánto fue el monto pagado sin considerar el IGV)
2.
3. Una fabrica que produce 246 litros de jugo diarios. Con 56 litros se llenan botellas de
0,5 litros de cada una y con el resto que queda en el deposito se llenan botellas de
2,5 litros ¿Cuántas botellas de jugo se llenan en total?
SOLUCIÓN
246 – 56 = 190, esto quiere decir que: con 56 litros llenarán botellas de 0,5 litros y con 190 litros llenarán botellas de 2,5 litros.
Para determinar la cantidad de botellas de cada capacidad que se llenan, se procede de la siguiente manera:
 |
País
|
Producción de café en millones de sacos de 60 kg
| ||
2012/2013
|
2015/2016
|
Incremento
| |
Brasil
|
50,8
|
49,4
|
-1,4
|
Vietnam
|
22,0
|
29,3
|
7,3
|
Colombia
|
9,50
|
13,6
|
4,1
|
Indonesia
|
50,8
|
11,8
|
-39
|
Etiopía
|
8,1
|
6,5
|
-1,6
|
49,4
|
–
|
50,8
|
=
|
- 1,4
|
La producción de café en Brasil fue disminuyendo, con respecto a los países de Vietnam y Colombia.
|
29,3
|
–
|
22,0
|
=
|
7,3
|
La producción de café en Vietnam fue en ascenso, con relación a los demás países.
|
13,6
|
–
|
9,50
|
=
|
4,1
|
La producción de café de Colombia también fue creciendo, pero menos que Vietnam.
|
11,8
|
–
|
50,80
|
=
|
- 3,9
|
Su producción de café de Indonesia fue mucho más la disminución, con relación a los demás países.
|
6,5
|
–
|
8,1
|
=
|
- 1,6
|
Etiopia fue disminuyendo, pero no es el último en la producción de café.
|
RETROALIMENTACIÓN:
DESAFIÓ PARA LA CASA:
ME PREGUNTO:
¿Qué aprendiste hoy?
¿Qué dificultades haz tenido?
¿Para qué te servirá lo aprendido?
MÁS INFORMACIÓN:
Te invito a ver este link PARA AQUELLOS ESTUDIANTES QUE TIENEN INTERNET EN CASA
¿Qué aprendiste hoy?






































































No hay comentarios.:
Publicar un comentario